こうした問題では、中心角を x∘ x ∘ とおいて方程式を作ってみましょう。 こうすると、このおうぎ形の面積を x x を用いて表せば 42 × π× x 360 4 2 × π × x 360 となります。 これが 12π 12 π になるので、次のようにして x x を求めることができます。まず、おうぎ形の面積に関しては (1)おうぎ形の面積「S=π・(r 2)・(x/360)」(円全体の面積に対する、中心角の割合分) (2)おうぎ形の弧の長さ「ℓ=2πr・(x/360)」(円周全体に対する、中心角の割合分) ということがそれぞれ言えますが、1辺の長さがa (cm)の正方形ABCDがあるとき,Bを中心とする半径a (cm)の円とDを中心とする半径a (cm)の円の共通部分の面積 (cm 2) ヒント 3 次の図のように半径10 (cm)の円の中に半径5 (cm)の円が2つ接しているとき,斜線部の面積 (cm 2) ヒント 図のように小さい円の半分を回転させると,凸の部分がちょうど凹の部分に重なるから,大きい円の面積の半分を求めるとよい (む

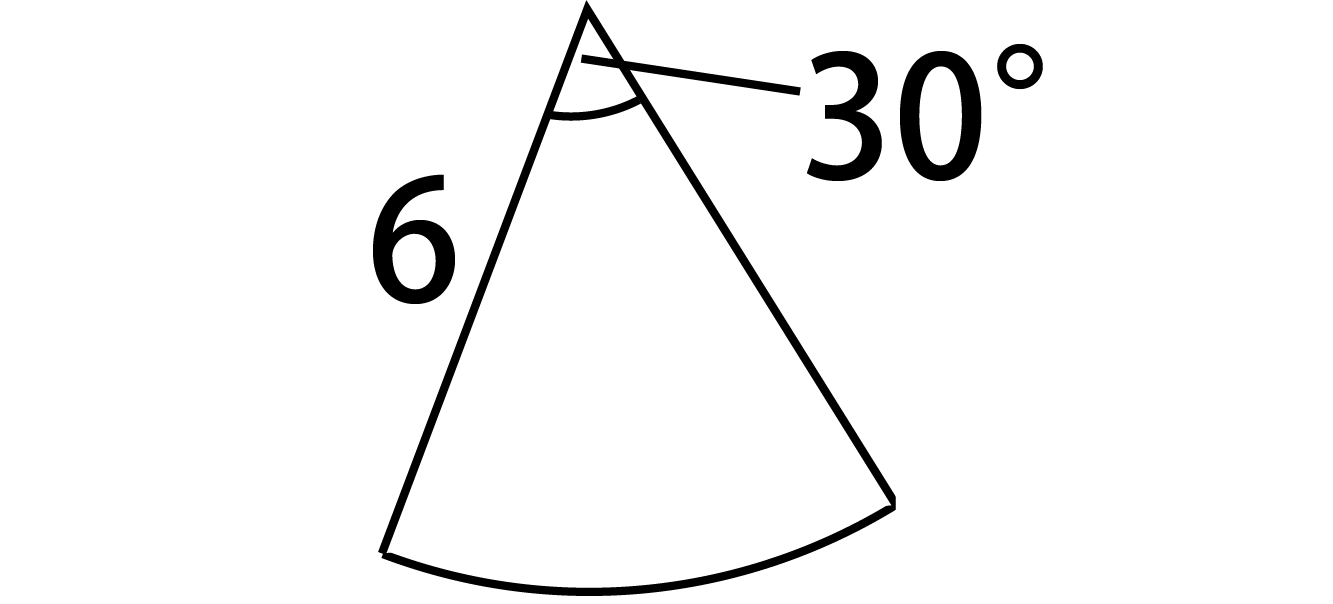
半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear
おうぎ形 面積 公式 高校
おうぎ形 面積 公式 高校-おうぎ形の面積の公式と求め方 教科書には扇形の面積や弧の長さを求める公式があります。 半径を\(\,r\,\),中心角 \(\,a^\circ\,\) として、これは4つすべてが おうぎ形 になっているよ。 ということは、 「全体の正方形」 から、 「おうぎ形4つ」 の面積をひけば、色のついた部分の面積が求められるんだ。



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
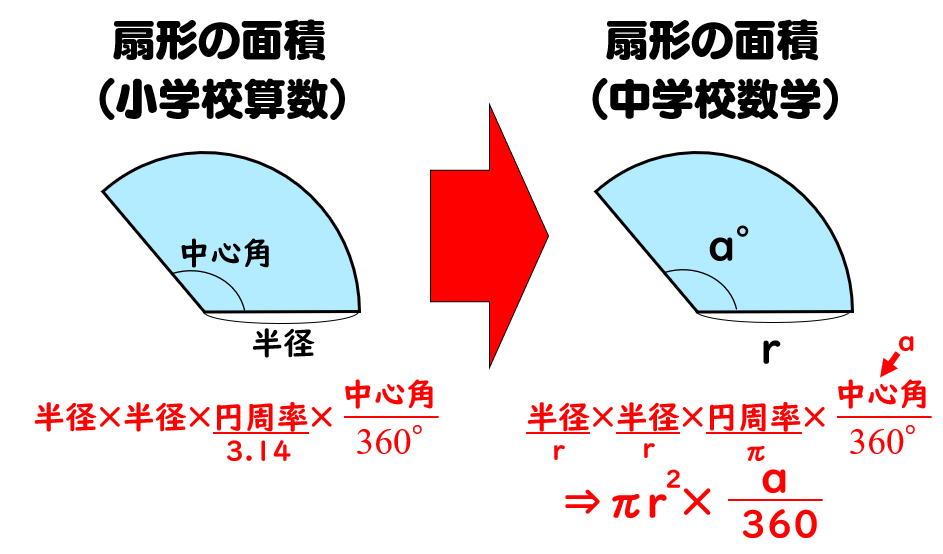
中学生公式確認問題①図形編 ①円の面積の公式 (半径をr、円周率をπ) ②円周の長さの公式 (半径をr、円周率をπ) ③おうぎ形の面積の公式 (半径をr、円周率をπ、中心角をx) ④おうぎ形の弧の長さの公式 (半径をr、円周率をπ、中心角をx)おうぎ形の公式 弧の長さ = 円周 × 中心角 360° 中 心 角 360 ° = 直径×314 × 中心角 360° 中 心 角 360 ° おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時に 三角形で高さにあたるものは、おうぎ形では、半径です。 このように見立てた場合、 三角形ならば面積は、1/2×底辺×高さ おうぎ形の面積は、1/2×弧×半径 同じ求め方ができるのです。 これは、度数法でも、多少複雑な過程を経れば導くことのできる公式です。 中学生でも、発展的な公式として学習します。 小学生でも、中学受験をする人は知っている
中学受験算数 おうぎ形の面積は 弧の長さ を使って5秒で計算しよう 円 扇形 の面積 周や弧の長さの公式 数学fun 扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援 中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 扇形 つまり、 この2つで考えるということですね。 作る比例式は、以下になります。 おうぎ形の弧の長さ 円の円周=おうぎ形の中心角:360 おうぎ形の面積 円の面積=おうぎ形の中心角:360 なんか見たことあるようなないような。 星野先生 求めるおうぎ形の面積は このおうぎ形の面積は、 元の円の面積の 6分の1 であるから $3\times3\times314\times\frac{\displaystyle 1}{\displaystyle 6}=\underline{471 cm^2 \dots Ans}$ おうぎ型・スーパー三角形の公式
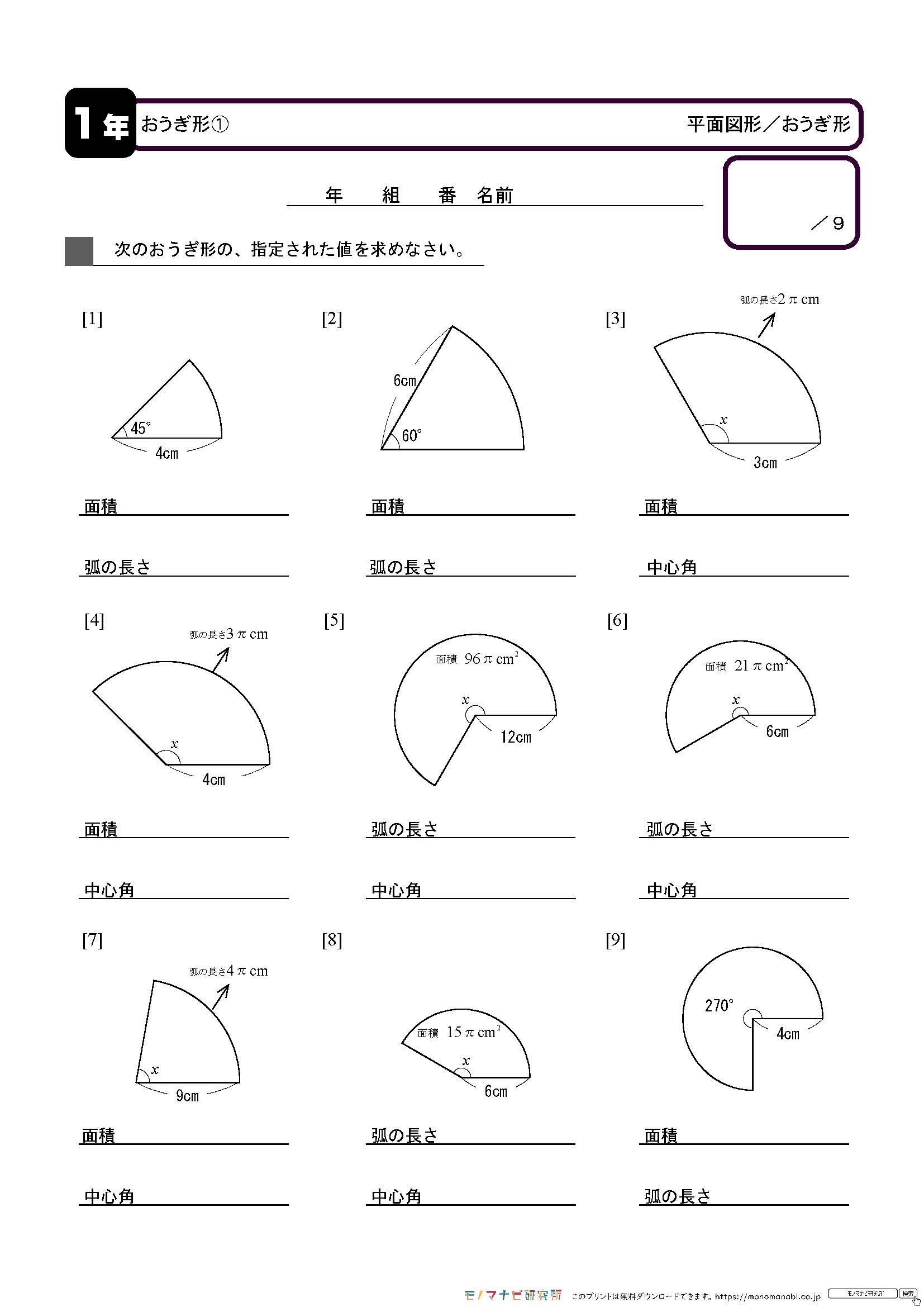
問題 面積がπ㎝²、中心角が40°であるおうぎ形の半径を求めなさい。 今度は面積が与えられているので おうぎ形の面積の公式に当てはめていきましょう。 すると、このような方程式ができあがります。 これを解いていきましょう! 両辺をπで割って 円とおうぎ形の作図の仕方や面積の求め方など そして回転体の表面積、面積の求め方など いろいろまとめてみました。 見にくくてすいませんt_tおうぎ形 1(2)解説 (2) 半径4㎝、弧の長さ2π㎝のおうぎ形がある。 ① 中心角は何度か。 ② 面積を求めよ。 半径4cmの円の円周は2×π×4=8π 弧の長さ2πなので 2π 8π = 1 4 このおうぎ形は円の 1 4 である



中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su



数 三角関数 円弧の長さと扇形の面積 オンライン無料塾 ターンナップ Youtube
中2数学 文字式の利用連続する3つの整数の和が3の倍数になる証明 中1数学 中学数学球の表面積の求め方の公式を1発で覚 おうぎ形の面積は、 「母線の長さ × 弧の長さ ÷ 2」 という公式で求めることが出来るのですが、その生徒は 「確かこう教わった気がする。あれ?こうじゃなかったっけ?わからん。けどなんとなくこの計算でやってた。 円とおうぎ形とピザの切り分け 中1の数学が、円とおうぎ形に入ってきました。 小学校までは、以下の公式で勉強します。 円周=直径 314 面積=半径 半径 314 ゆとり時代は円周率はおよそ3なんて言われましたが、今は314が復活しており、それに伴い



Q Tbn And9gcqwkabdudclaf 47vgw O93wu16c0ercc O5o6eo6xp177ses0w Usqp Cau



半径8cm 中心角135 のおうぎ形の弧の長さと面積を求めてくださ Yahoo 知恵袋
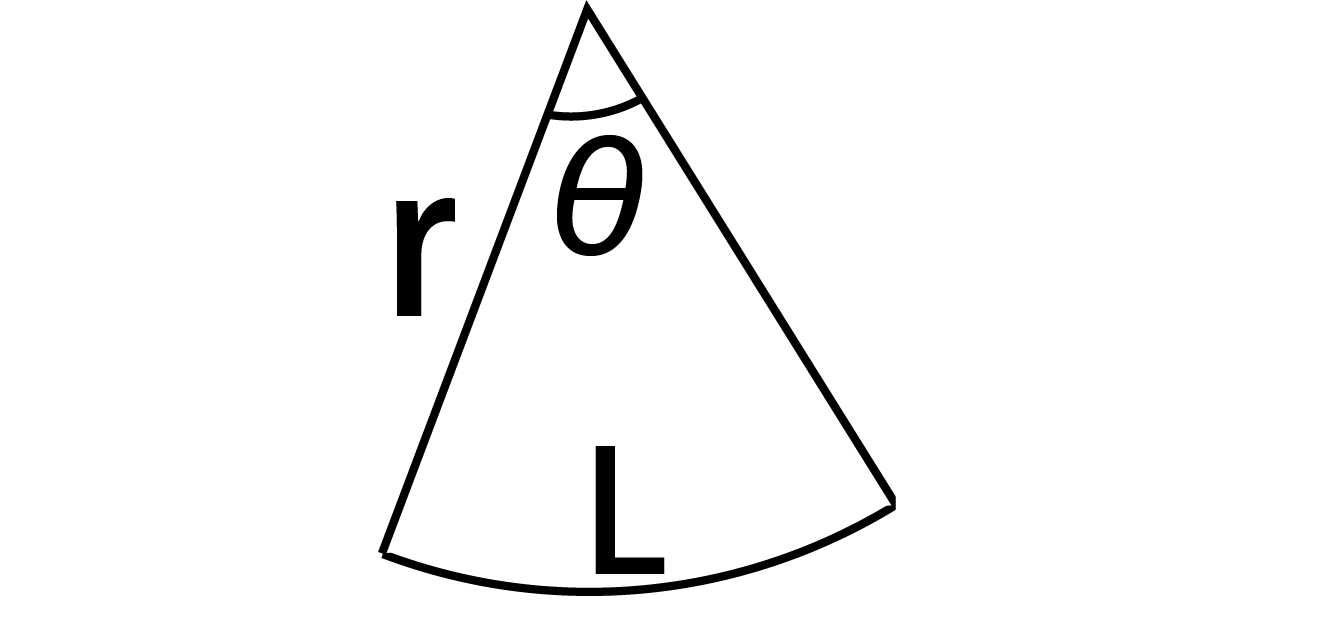
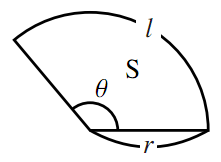
⑴は「円の公式」を使っています ⑵の図形は「半円」なので、 公式の後に「÷2」で半分にしています ⑶の図形は 「円を4等分した おうぎ形」なので 公式の後に「÷4」で求めています ⑷は求める図形の左側を移動すると まとめ:扇形の面積は「おうぎ形パワー」を円にかける 扇形の面積の求め方はどうだった? ? 円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。 S = πr² × α / 360 「円とおうぎ形」がテストにでるときに確認したいね^^ おうぎ形のまた面積の公式にはもう一つあります。これも覚えておくと便利でしょう。 半径の長さr、弧の長さLのおうぎ形の面積Sは、$$\begin{eqnarray*} && {\Large S=\frac{1}{2} rL}\ \end{eqnarray*}$$ この公式はおうぎ形の中心角が与えられてないときに役立ちます。




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



1
おうぎ形の孤の長さ・面積の公式です 学年 中学全学年, 単元 おうぎ形, キーワード 公式,面積,孤の長さ おうぎ形の面積を求める公式 面積=円の面積×中心角の割合 半径5cm、中心角36度のおうぎ形の面積は何cm 2 計算方法は加減法または代入法で選択でき、途中式も表示されます。 おうぎ形の面積 $$\pi r^2 \times \frac{a}{360}$$ 円の公式を覚えていれば おうぎ形の公式は\(\times \frac{a}{360}\)をくっつけるだけで作ることができますね!




扇形の面積の求め方 公式と計算例
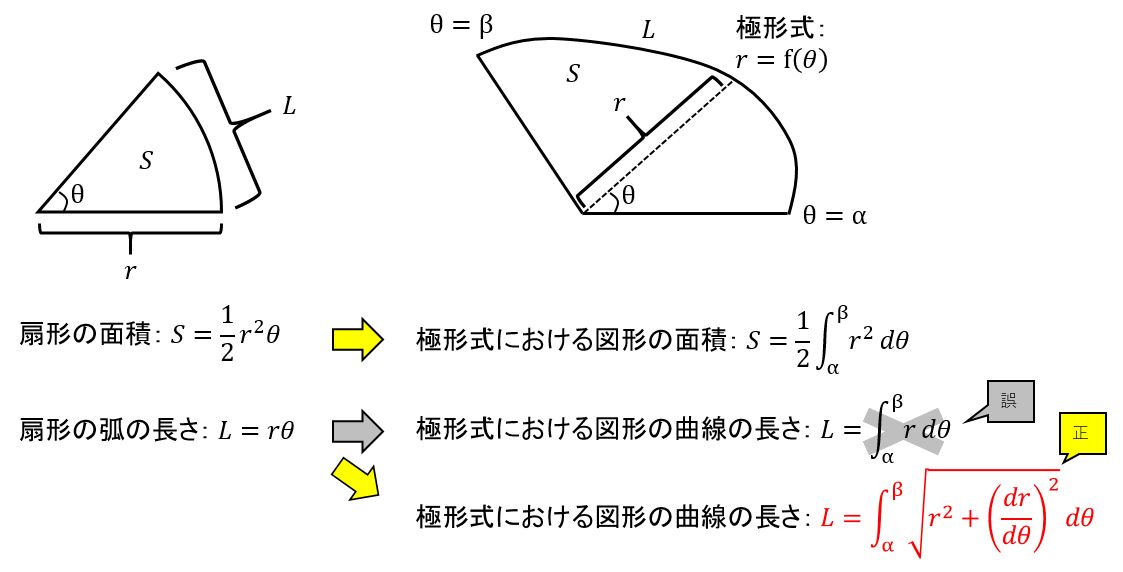



Lさんのツイート 今ミスしたことをまとめました 極形式について 面積は扇形から公式が作れるのですが 曲線の長さは扇形から作れません D 作れない理由は Rとr 2における近似レベルの違いな気がしますが 詳細は調べてません 数学 数検 高校
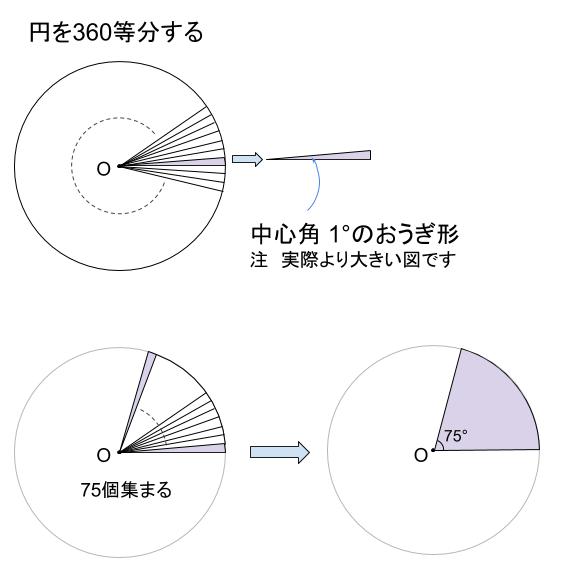
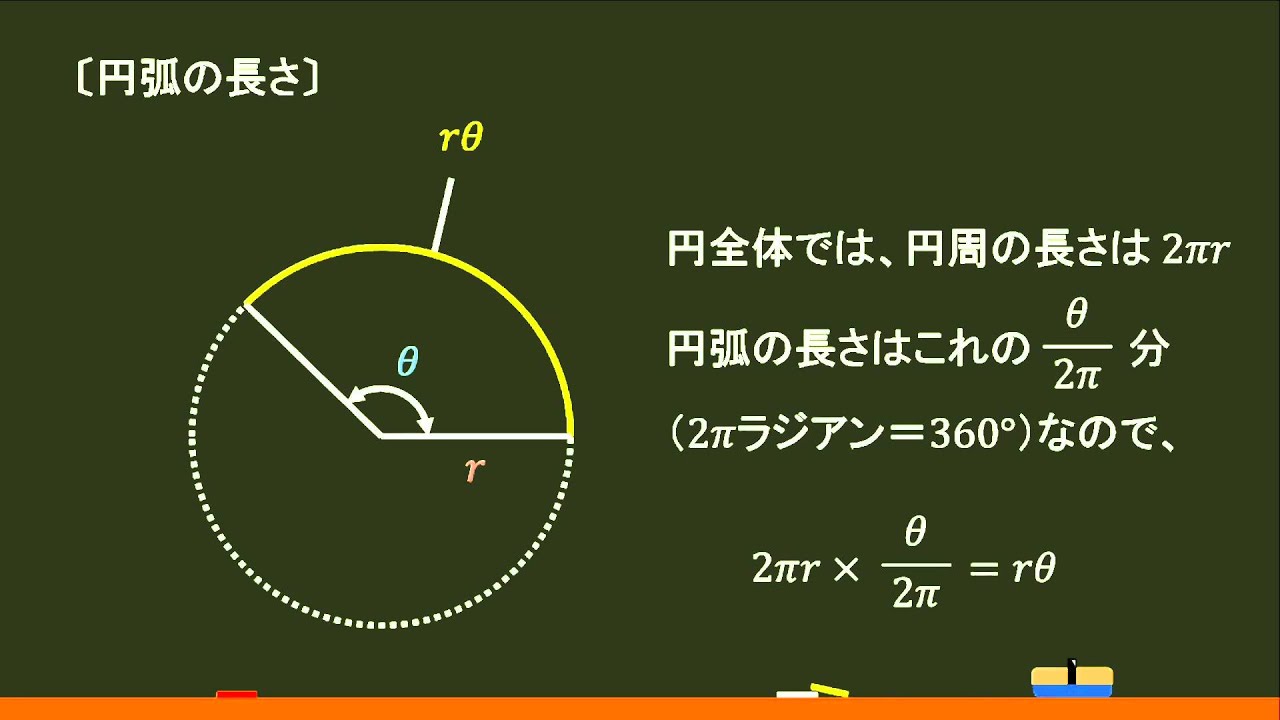
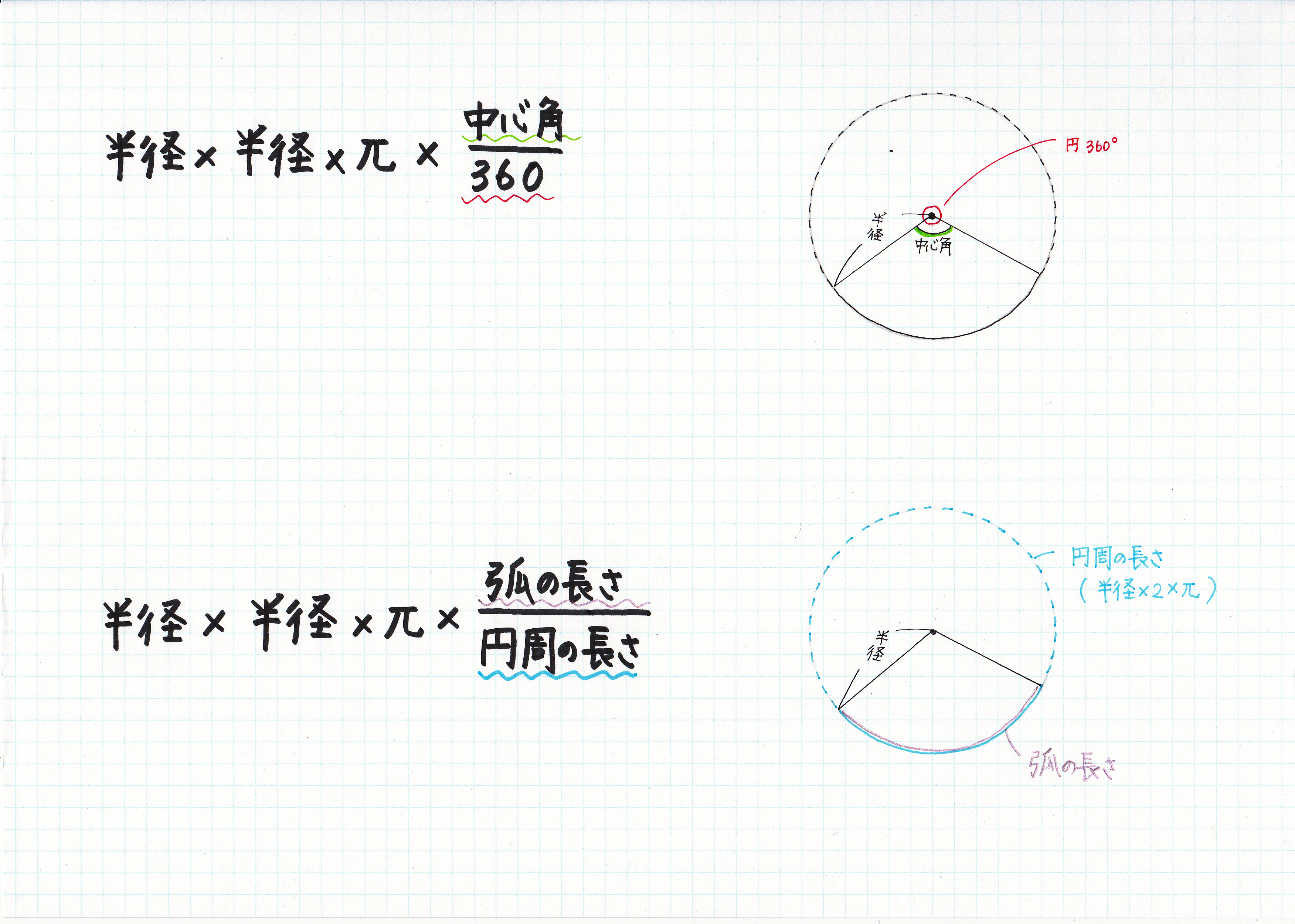
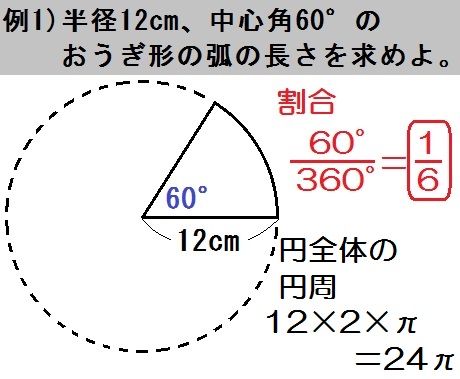
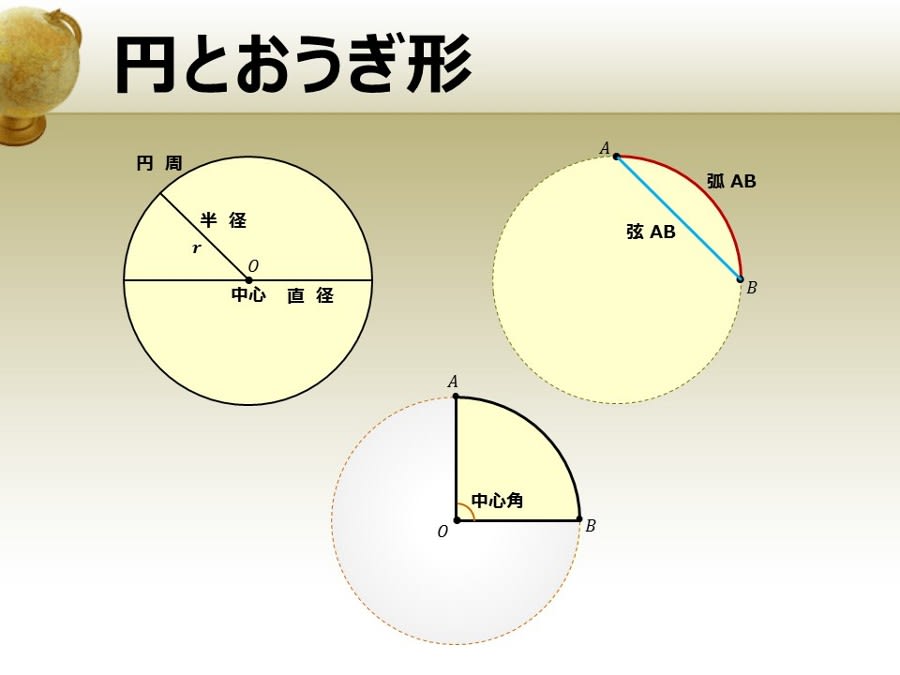
おうぎ形の弧の長さや面積は中心角に比例するので, おうぎ形の弧の長さや,面積を求めるには, 円周の長さや,円の面積に 中心角 360° をかければよい。 半径rで中心角がaのおうぎ形 弧の長さ l = 2πr × a 360 面積 S = πr2 × a 360 例半径18cm, 中心角40°の面積:s=π𝑟2 ・おうぎ形の定義をノートに記入す る。 定義 ・おうぎ形とは、円の2つの半径と 弧で囲まれた図形である ・おうぎ形の公式をノートに記入 する。 ・公式 面積=( 半径)×( ×π ×中心角/360 ・弧の長さ=(直径)×π ×中心角/360おうぎ形の面積は 円の面積 から求めるよ。 円の面積の公式は、 「(半径)×(半径)×π」 だよ。 おうぎ形の 中心角は60° だから、円全体の360°のうちの60°分が切り取られているわけだね。 公式を使うと次のように計算できるよ。



おうぎ形の面積の公式について 現役塾講師のわかりやすい中学数学の解き方




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく
面積は「9π㎠の半分の「\(\frac{9}{2}\)π㎠」になるね。 4分の一だったら? 3分の2だったら? とにかく、 もとの円の円周や面積を求めれば、 もとの円と比べておうぎ形がどのくらい残っているかによって、 おうぎ形の面積や円周も求めることができるんだね。 正方形の面積は、ひし形の公式によって「6㎝×6㎝×1/2=18㎝2」 正方形の一辺をAとした場合、正方形の面積はA×A=18㎝2 Aは求めるおうぎ形の半径なので、おうぎ形の面積は、A×A×314×90/360 ②よりA×A=18なので、18×314×1/4=1413㎝2おうぎ形は、円を切り取った一部だね。 つまり、円周を切り取った一部が「おうぎ形の弧」なんだよ。 さらに、円の面積を切り取った一部が「おうぎ形の面積」。 そして、円の中心角360°の一部を切り取ったものが「おうぎ形の中心角」。 これらのことから、覚えておきたいポイントは次のようになるんだ。 POINT 「弧の長さ」や「面積」は、円の公式から求める




円の面積 公式




おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ
〔質問〕 円の半径・円周、おうぎ形の弧の長さ・面積、円柱・円錐の面積、球の面積など複雑な公式が多くて、なかなか全部覚えられません。なにかいい覚え方はありますか? 〔回答〕 「丸暗記」する項目と、そこから「その都度導き出す つぎに面積。 おうぎ形って円の一部だから、おうぎ形の面積=円の面積の一部です。 だから(円の面積)× \(\frac{1}{4}\) をすればいい。 円の面積は $$ 6 \times 6 \times \pi = 36 \pi $$ よって、求めるおうぎ形の面積は $$ 36 \pi \times \frac{1}{4} = 9 \pi $$ 答.\(9 \pi \) ㎠ と出ます。




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




高校入試の直前対策として おうぎ形のまとめ が ワード数学ラボラトリ Microsoft Word And Math فيسبوك



おうぎ形の面積の公式 算数の公式




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



中学数学 平面図形 のコツ 円とおうぎ形



モノマナビ研究所




中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



高校入試と 円とおうぎ形 中学生 受験対応 英語 数学 学習講座



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su




至急です 扇形の面積の公式を使って色がついている部分の面積を求めなさいという問題です Clear




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題



高校入試数学 おうぎ形についての公式まとめとその練習問題




おうぎ形



扇 おうぎ 形の面積を求める公式と弧の長さの求め方




おうぎ形の面積 弧度法との関連から眺める 身勝手な主張




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




応用 おうぎ形と正方形の面積 なかけんの数学ノート




裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 2 Youtube




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear



円 扇形 の面積 周や弧の長さの公式 数学fun



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext




三角形と扇形の面積 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




数学パズル 意外と悩むおうぎ形の面積問題 ひらめいたらスッキリします 暇つぶしに動画で脳トレ




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題
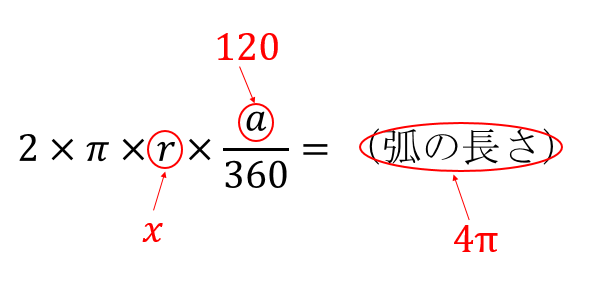



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
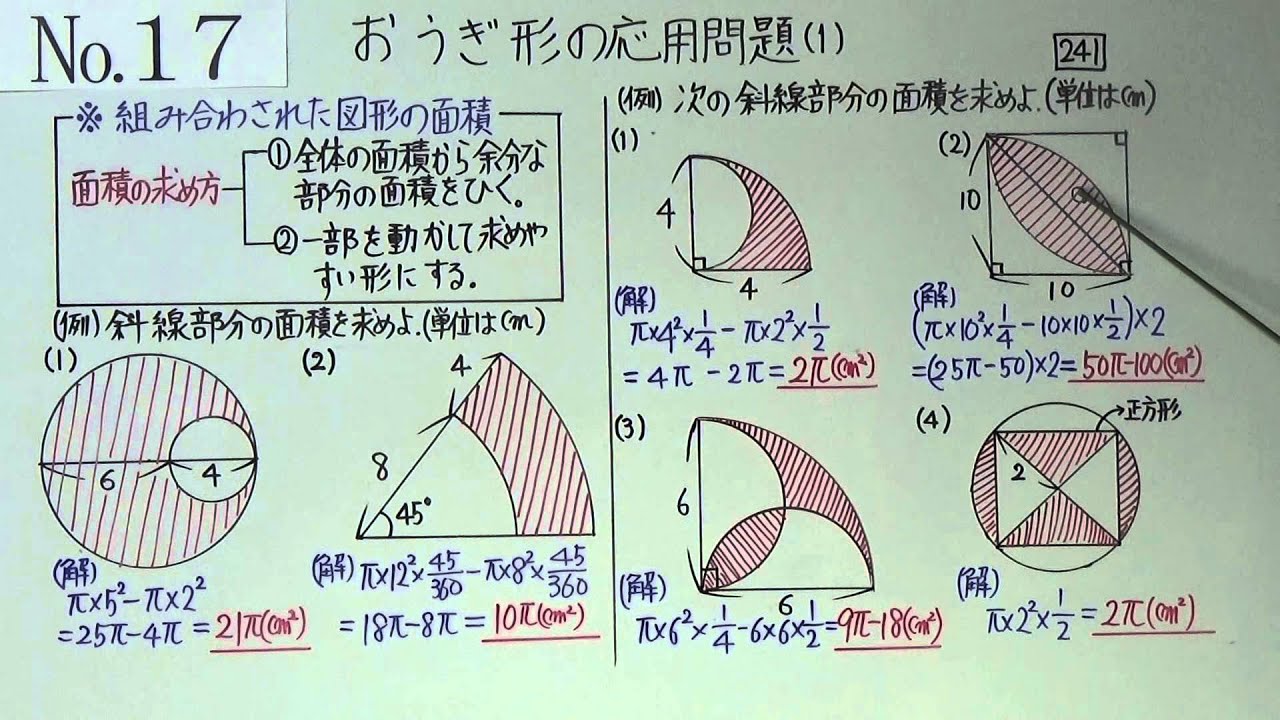



中1 17 2 おうぎ形の応用 1 Youtube
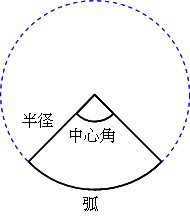



Mathematics 平面図形 おうぎ形 働きアリ




高校入試の直前対策として おうぎ形のまとめ が ワード数学ラボラトリ Microsoft Word And Math فيسبوك
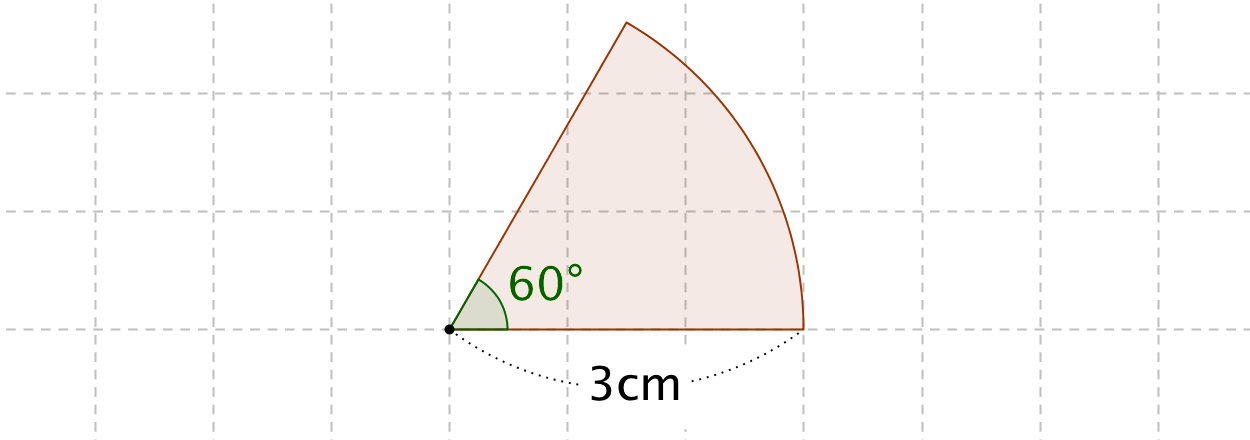



おうぎ形の面積の公式 算数の公式




円 扇形 の面積 周や弧の長さの公式 数学fun




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ



問題93おうぎ形の面積
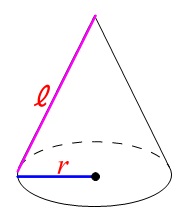



扇 おうぎ 形の面積を求める公式と弧の長さの求め方




中1 中1 数学 範囲 おうぎ形の中心角の求め方 大放出ぅ 中学生 Clear




公式を図解 すい体の体積 円すいの表面積の求め方




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




高校入試でよく出る数学の公式10選 Part1 個別学習塾ナレッジ



1




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




山と数学 そして英語 高校数 三角関数 おうぎ形の弧の長さと面積




中学数学重要公式集 高校入試対策 プロシードネットショップ




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su




おうぎ形




高校数学 極方程式で表された関数の面積 扇形分割積分 正葉曲線r Sin28 受験の月



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




平面図形 おうぎ形の中心角 中学数学 定期テスト対策サイト




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




帰国子女高校受験 数学を得意科目にして合格を目指す 中学1年生 幾何編 海外 帰国子女向けオンライン家庭教師 Tck Workshop




おうぎ形の面積と弧の長さの公式 全国 中学数学ができるようになるブログ



Images Of 長弧 Japaneseclass Jp




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり




三角形面積求め方 三角形とは 面積公式 角度 辺の長さ 重心 比の計 Jbqhd




おうぎ形と円すい 高校入試問題 数学 を毎日解いてみよう




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
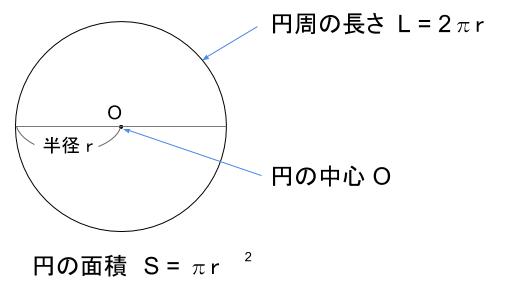



中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su




高校受験の入試問題によく出る 扇の面積を使った応用問題 中学数学 By じょばんに マナペディア




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト



高校入試数学 おうぎ形についての公式まとめとその練習問題
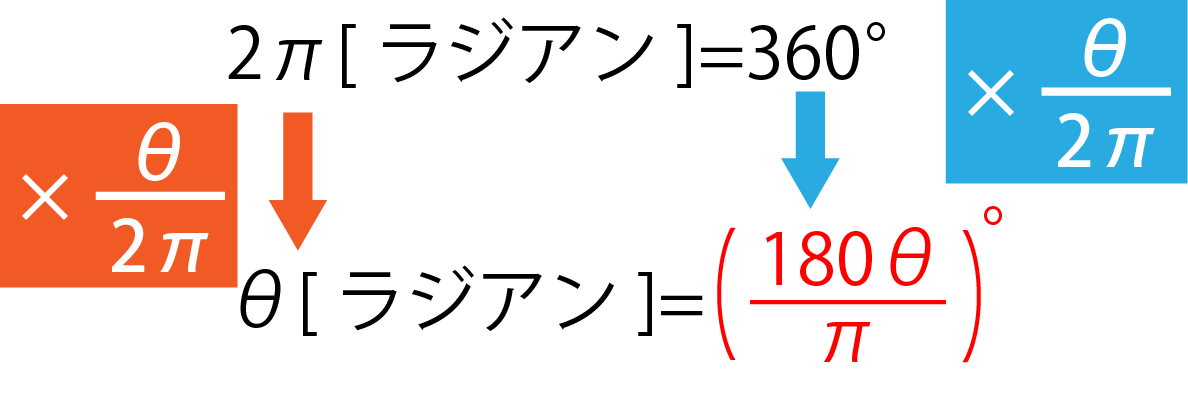



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ




扇形の弧の長さ 扇形の面積 弧度法 一夜漬け高校数学274 三角関数 Youtube




数学質問 おうぎ形の面積の公式について Youtube



Search Q E5 86 86 81 Ae E9 9d E7 8d Tbm Isch



高校入試数学 おうぎ形についての公式まとめとその練習問題




高校受験数学 円とおうぎ形 弧の長さと面積 の授業映像 プリント無料配布 Youtube スタディカフェ
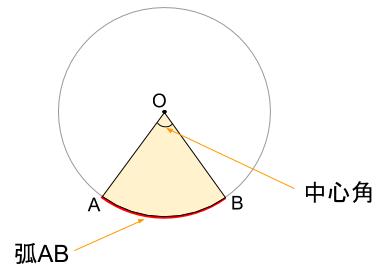



中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su




円とおうぎ形 応用 無料で使える中学学習プリント




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく




中1数学のおうぎ形の公式が覚えられません そろそろテストなのでやばいんです 今はとに Clear




高校入試対策数学 円錐に関する対策問題 Pikuu




標準 おうぎ形と正方形の面積 なかけんの数学ノート




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




B Descubre Como Resolverlo En Qanda




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




扇 おうぎ 形の面積を求める公式と弧の長さの求め方




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張




中1数学 おうぎ形の公式 例題編 映像授業のtry It トライイット




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか
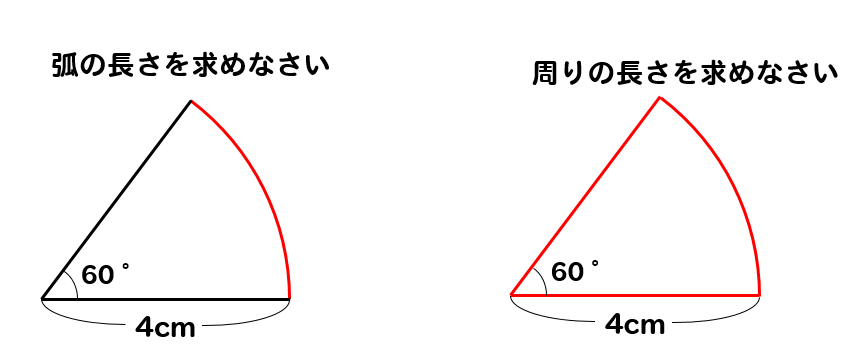



おうぎ形 注意 周りの長さを求める公式を解説 数スタ




B Descubre Como Resolverlo En Qanda



0 件のコメント:
コメントを投稿