Simple and best practice solution for X^2(p2)x2p1=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If the difference of the roots of the equation , x2 p x q = 0 be unity , then (p2 4q2) equals to (A) (1 2q)2 (B) (1 2q)2 4 (p q)2 (D) 2 (p q)2Answer to 2 i) Selve lýt²x²) p 2 x y z q 2 x 2 = 0 Who are the experts?

How To Complete The Square And Write A Quadratic In The Form X P 2 Q Youtube
P 2 x 2 p 2-q 2 x-q 2 0
P 2 x 2 p 2-q 2 x-q 2 0- We have the quadratic equation in x, x^2 mx m^2 a = 0, and its given that it has roots p and q So, sum of roots = p q = m/1 = m product of roots = pq = m^2 a We have to find the value of p^2 q^2 pq p^2 q^2 pq = (p q)^2 pq Now, we'll use the values of (p q) and pq we calculated above; Divya Janjua, added an answer, on 27/2/13 Divya Janjua answered this p2x2 (p2q2)xq2=0 p2x2 p2x q2x q2 = 0 p2x ( x 1 ) q2 ( x 1 ) = 0 ( x 1 ) = 0 or ( p2x q 2 ) = 0 therefore x = 1 or x = q2 / p2




Example 24 If P Q R Are In Gp And Equations Px2 2qx R 0
Nature of the roots for a quadratic equation a2 bxc = 0 can be determined by its Discriminant, D = b2 −4acHere, D = p2 −4qSince, the roots are not realTherefore,DSolve the following quadratic equation for x p^2x^2 (p^2 q^2) x q^2 = 0 ← Prev Question Next Question → 0 votesExperts are tested by Chegg as specialists in their subject area
Solve using quadratic formula p^2X^2(p^2q^2)Xq^2=0Here (^)means square 2 See answers Brainly User Brainly User Hope u like it mark it= (m)^2 (m^2 a) = m^2 m^2 a = a Hence, the value of p^2 q^2The PDE p^2 q^2 = x^2 y^2 for the function U(x,y) with p =U_x , q =U_y written as p^2 x^2 = q^2 y^2 suggests to assume U(x,y) = F(x) G(y) From the equation obtain the separation F'(x)^2 x^2 = G'(y)^2 y^2 =K with K constant Follows the equations (assume K>0) F'(x) = (x^2 K)^1/2 G'(y) = (y^2 K)^1/2 , y^2 K >=0
Chapter 1 (maths 3) 1 CHAPTER 1PARTIAL DIFFERENTIAL EQUATIONS A partial differential equation is an equation involving a function of two ormore variables and some of its partial derivatives Therefore a partial differentialequation contains one dependent variable and one independent variable Here z will be taken as the dependent variable andSedan byter du tecken på द्विघात सूत्र का प्रयोग करके p^(2)x^(2)(p^(2)q^(2))xq^(2)=0 का हल कीजिए। Updated On 212 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student



View Question The Number 1750 Can Be Written As 2 X 5 X Q Where P And Q Are Prime Numbers Work Out The Value Of P And The Value Of Q



Madasmaths Com Archive Maths Booklets Basic Topics Various Polynomials Exam Questions Intro Pdf
Show that p, q = p ( 0) q ( 0) p ( 1) q ( 1) p ( 2) q ( 2) defines an inner product on the space P 2 of polynomials of degree at most 2 Here's my solution Therefore, this defines the inner product on the space of P 2 Apply the GramSchmidt algorithm to the basis { 1, x, x 2 } for P 2 to construct a basis { p 0, p 1, p 2 } that is 0 Find the solution of p 2 q 2 = 1 that passes through the circle x 2 y 2 = 1, z = 1 Here, p = ∂ z ∂ x and q = ∂ z ∂ y Using Charpit's method, we can find the general solution to be, z = a x y 1 − a 2 b where a and b are arbitrary constantsLearn with Tiger how to do p^2q^2/pq/p/p^2qp fractions in a clear and easy way Equivalent Fractions,Least Common Denominator, Reducing (Simplifying) Fractions Tiger Algebra Solver




Improved Design And Analysis Of Practical Minimizers Biorxiv



Using Shridhar Acharya Formula Solve The Following Quadratic Equations P 2x 2 P 2 Q 2 X Q 2 0 Sarthaks Econnect Largest Online Education Community
Solve simultaneously by adding the two equations p^2 q^2 = 16 p^2 q^2 = 8 ——————– 2(p^2) = 24 From this we can work out p p^2 = 12 p = sqrt(12) p = 2(sqrt(3)) This is roughly 346 Therefore from the first equation we can sub in to get (2(s また a=0 のとき I (0)=0 となります。 I (a) を a で微分します。 I' (a)=\displaystyle\int_0^ {\infty} \frac {p^2x^2} { (1ap^2x^2) (q^2x^2)}dx 被積分関数を部分分数分解します。 \begin {alignat} {2} &\frac {AxB} {1ap^2x^2}\frac {CxD} {q^2x^2}=\frac {p^2x^2} { (1ap^2x^2) (q^2x^2)}\\ &\\ & (AxB) (q^2x^2) (CxD) (1ap^2x^2)=p^2x^2\\ (xp)^2 = (xq)^2 just take the root, and you have either xp = xq so no solution unless p=q, in which case there are infinitely many solutions OR xp = (xq) 2x = qp x = (qp)/2 Or, you could have expanded at the start (xp)^2 = (xq)^2 x^2 2px p^2 = x^2 2qx q^2 2(qp)x = q^2 p^2 = (qp)(qp) 2x = qp unless q=p x = (qp)/2



Http Www Columbia Edu Kr2248 4109 Chapter5 Pdf




Charpit Method Non Linear Pde Mathematics Stack Exchange
Homework Statement Express x^2 10x in the form (xp)^2 q State the value of P and Q The Attempt at a Solution I don't know! x^2 px q has roots alpha, beta We have to form an equation whose roots are q/(p α) and q/(p β) Sum of roots= q/(p α) q/(p β) = p Product of roots= q/(p α) * q/(p β) = q The answer is x^2pxq = 0 Now, since a quadratic equation has only two roots, all we can say now is that "α and β equals q/(p α) and q/(p β)" Actually, it was the same pair of rootsYou need to write this in the form You do this by taking the coefficient of x, which is 6, and take half of it, and square, which is 9 The trick is to add 9 and subtract 9 on the right side, in order to do what needs to be done, but keep the equation the same Notice that the quantity is a perfect square trinomial, and




Chapter 1 Maths 3
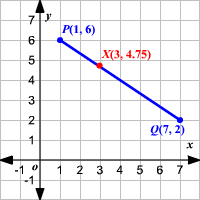



Partitioning A Segment In A Given Ratio
1 See answer amazingaryan04 is waiting for your help Add your answer and earn points ashapuri1977 ashapuri1977P(q(x)) p ( q ( x)) Evaluate p(q(x)) p ( q ( x)) by substituting in the value of q q into p p p(2x−1) = −2(2x−1) 1 p ( 2 x 1) = 2 ( 2 x 1) 1 Simplify each term Tap for more steps Apply the distributive property p ( 2 x − 1) = − 2 ( 2 x) − 2 ⋅ − 1 1 p ( 2 x 1) = 2 ( 2 x) 2 ⋅Factor p^2q^2 p2 − q2 p 2 q 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( a b) where a = p a = p and b = q b = q (pq)(p−q) ( p q) ( p q)




If P And Q Are Roots Of The Quadratic Equation X 2 Mx M 2



The Coefficient Of X In The Quadratic Equation X 2 Px Q 0 Was Taken As 17 In Place Of 13 Its Roots Were Found To Be 2 And 15 How Do You Find The Original Roots
在x 趋于0的时候, 分子分母都趋于0, 而 √(x^2p^2) p=x^2 / √(x^2p^2) p √(x^2q^2) q=x^2 / √(x^2q^2) q 所以得到 निम्न द्विघाती समीकरण x के लिए हल कीजिए p^(2)x^(2)(p^(2)q^(2))xq^(2)=0 Updated On 309 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!Watch Video in App



Www Imo Official Org Problems Imo08sl Pdf




P 2 X 2 P 2 Q 2 X Q 2
(q x 2 − 2 q x 2 q) p (− x 1) p 2 − q 2 x q 2 = 0 All equations of the form ax^{2}bxc=0 can be solved using the quadratic formula \frac{b±\sqrt{b^{2}4ac}}{2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction Best Answer Notice that (p q) 2 = p 2 2pq q 2 But notice that (q p) 2 is exactly the same result (prove this for yourself) So all we really need to do is to just double the first result, and we get 2p 2 4pq 2q 2 as Aziz found !!!Rewrite, p 2 p 2 x − q 2 x − q 2 = 0 ⇒ p 2 x (x 1) − q 2 (x 1) = 0 ⇒ (x 1) (p 2 x − q 2) = 0 ⇒ If x − 1 = 0 or (p 2 x − q 2) =0 ⇒ x = − 1 or x = p 2 q 2



Http Cloudportal Sathyabama Ac In Coursematerial Staging Uploads Smt54 Pdf




Example 24 If P Q R Are In Gp And Equations Px2 2qx R 0
p 2 x 2 (p 2q 2)xq 2 =0 D=b24ac =(p 2q 2)2 4p2 x q2 =p4q42p2q2 4p2q2 =p4q42p2q2 =(p2q2)2 we know x= b undr root D/2a =p2q2p2q2/2p2 =2q2/2p2 =q2/p2 also x=b undr root D/2a =p2q2p2q2/2p2Simple and best practice solution for p^2x^2(p^2q^2)xq^2=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy all other terms to the right Add 'q 2 ' to each side of the equation p 2 q 2 x p 2 x 2 1q 2 q 2 = 0 q 2 Combine like terms 1q 2 q 2 = 0 p 2 q 2 x p 2 x 2 0 = 0 q 2 pGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
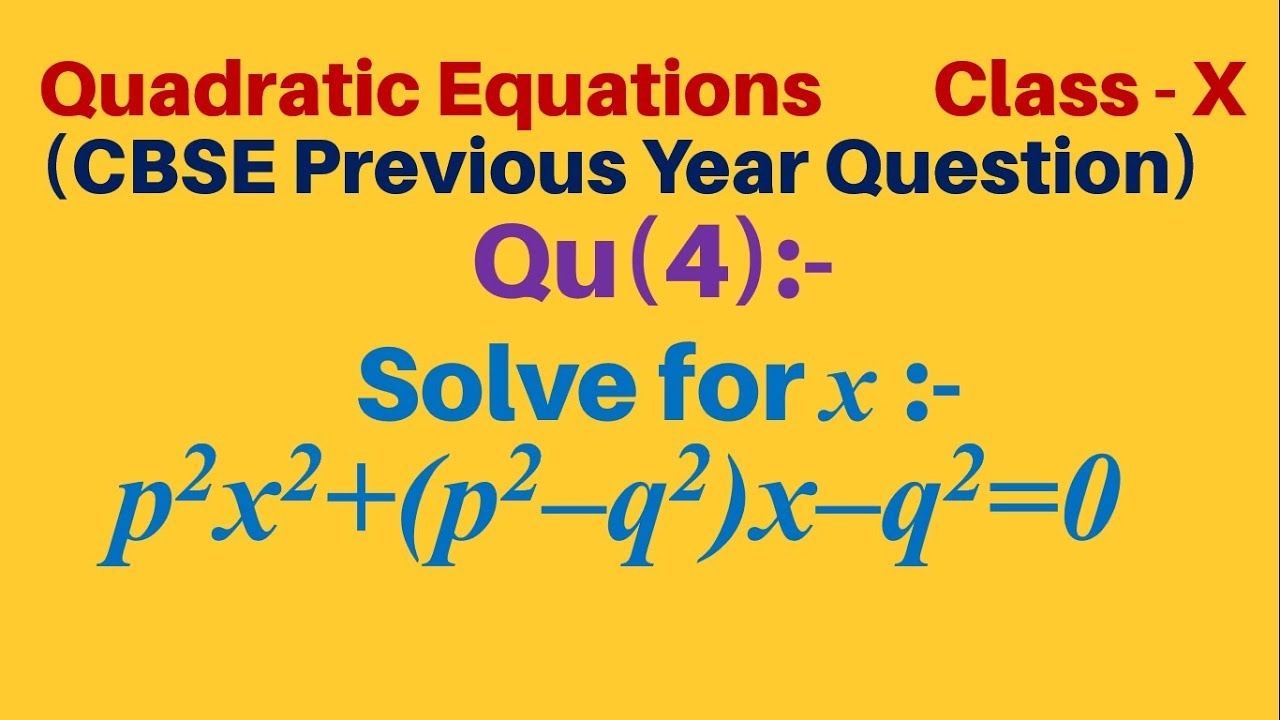



Q4 Solve For X P2x2 P2 Q2 X Q2 0 P Square X Square Bracket Of P Square Q Square Youtube




Solution Of A Partial Differential Equation
EduRev Class 10 Question is disucussed on EduRev Study Group by 1003 Class 10 StudentsX2 p2 y2 q2 = 1 x 2 p 2 y 2 q 2 = 1 We can find p by first transposing this equation So here we transfer the second term to the right side but this time flip the sign such as its negativeI don't get it because when I times out the brackets p will always be a number, and there are no numbers that
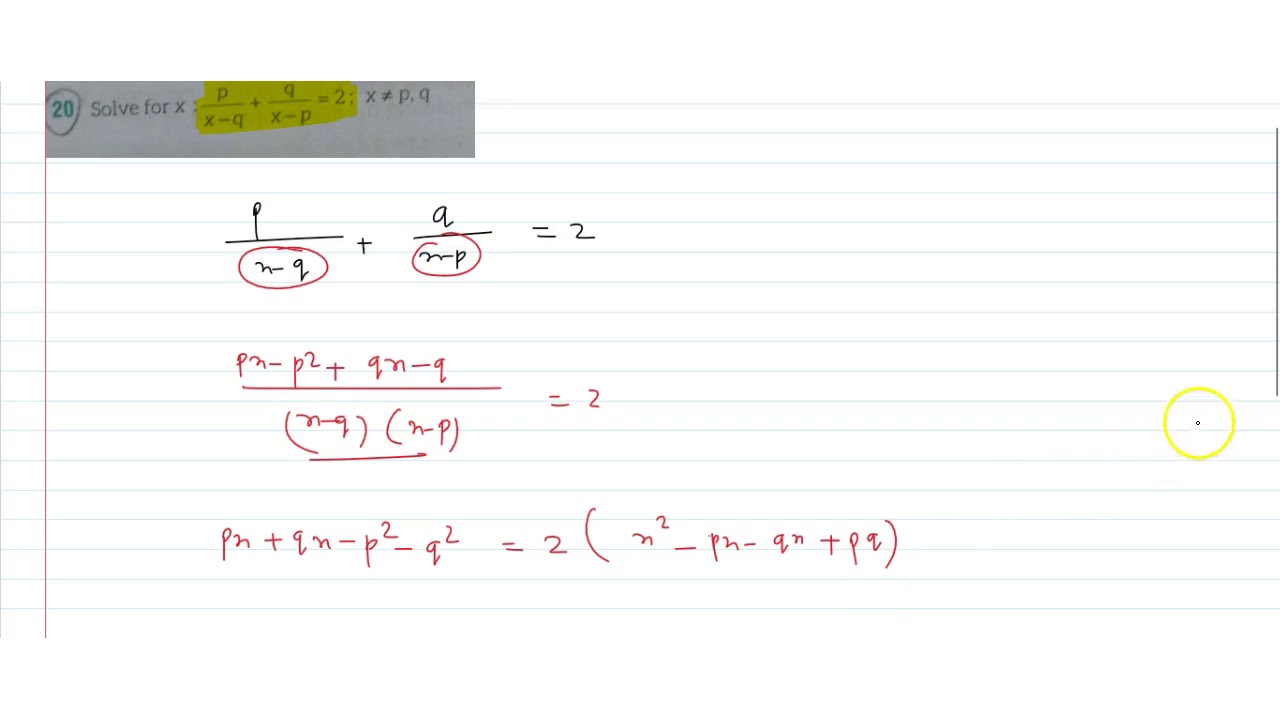



Solve X P X Q Q X P 2 X P Q Youtube



1
P/xq q/xp = 2 , x=?Why create a profile on Shaalaacom?What is the method for these sorts of questions the actual question I'm trying to tackle is express 3x^2 5x1 in the form p(xq)^2r and to be hones




Finding Features Of Quadratic Functions Video Khan Academy




On Controlling The P2 O2 Phase Transition By Optimal Ti Substitution On Ni Site In P2 Type Na0 67ni0 33mn0 67o2 Nnmo Cathode For Na Ion Batteries Sciencedirect
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more Tigster 252 Postad 16 sep 1510 Redigerad 16 sep 1513 Din kvadratkomplettering är inte helt rätt, x2 px q = (x p 2)2 (p 2)2 q Det stämmer alltså inte att (1)2 = 1 Sen borde du flytta över det utanför kvadraten till HL, dra roten ur båda ledP iii Second Moment E X 2 q p 2 q 2 p 2 iv Variance V X q p 2 v CDF Complement from STATISTICS sta564 at University of Southern Maine



Solution Solve X Using Quadratic Formula P2x2 P2 Q2 X Q2 0




Chapter 1 Maths 3
Dvs x p 2 y q 2 1 som är ekvationen för cirkeln med radien a och centrum i punkten (p,q) Anmärkning 2 Cirkelns ekvation definierar två explicita funktioner ( och därmed två funktionskurvor) som vi får genom att lösa ut y ur ovanstående ekvationAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators Jul 24,21 If p2x2 – q2 = 0, then x =?a)± q / pb)± p / qc)pd)qCorrect answer is option 'A' Can you explain this answer?



Www Parkhighstanmore Org Uk Attachments Download Asp File 1514 Type Pdf



Http Www Pnp Physics Ox Ac Uk Mjohn Notes Matterlectures Pdf
Get an answer for 'Express x^2 8x 17 in the form (xp)^2 q, where p and q are integers and find the minimum value of x^2 8x 17' and find homeworkExpress x^2 7x 2 in the form (x p)^2 q , where p and q are rational numbers This is an example of completing the squareIf we expand (x p)^2 q, we will have x^2 2px p qNow we can use algebra to work out what p and q are from the following equation x^2 7x 2 = x^2 2px p^2 q 7x 2 = 2px p^2 q We can force an6साल में 6बार बैन, फिर भी ज़िद के पक्के देश और धर्म विरोधी मीडिया के विरुद्ध




Solve Quadratic Equations Using The Quadratic Formula Elementary Algebra



2
please solve it 3 (2x1)^25 (2x1)4=0 1/ (2ab2x)=1/2a1/b1/2x I hope u understand the questionin words it is one upon twice of a plus b plus twice of x equals one upon twice of a plus one upon b plus one upon twice of x (x^2x)^25 (x^2x) 4=0 25x^230x7=0 solve by formula x\33\6x=2 (6x)\15 x2 (3–2a)x – 6a=01 Inform you about time table of exam 2 Inform you about new question papers 3 New video tutorials information$$\alpha, \beta $$ are roots of the equation $$(a1)^{2} (2a3)x(3x4)= If $$\alpha \beta =2$$, then $$\alpha, \beta=$$




Worked Example Completing The Square Leading Coefficient 1 Video Khan Academy



A P2 Type Na0 44mn0 6ni0 3cu0 1o2 Cathode Material With High Energy Density For Sodium Ion Batteries Journal Of Materials Chemistry A Rsc Publishing
Eftersom pqformeln utgår från x 2 p x q = 0 x^2pxq=0 och din ekvation är x 23 x10 = 0 x^23x10=0 så gäller att p =3 p=3;Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations p^2x^2(p^2q^2)xq^2 so that you understand better




If The Roots Of The Quadratic Equation P Q R X 2 Q R P X R P Q 0 Are Equal Show Then 1p 1r 2q Mq Find M



Qualifications Pearson Com Content Dam Pdf A level Mathematics 13 Exam materials C2 June 05 Mark Scheme Pdf



Solve The X By Quadratic Formula P 2x 2 P 2 Q 2 X Q 2 0 Youtube




Solve P X Q Q X P 2 Maths Quadratic Equations Meritnation Com



Www Jstor Org Stable



Studywell Com Wp Content Uploads 21 03 Differentiationexamquestions Pdf




How To Complete The Square And Write A Quadratic In The Form X P 2 Q Youtube




Mas111 15 16 Exam Studocu



Using Quadratic Formula Solve The Following Quadratic Equation P 2x 2 P 2 Q 2 X Q 2 0 Sarthaks Econnect Largest Online Education Community



Math 1 Chapter 3 Quadratic Functions Ppt Download



Mcq Questions For Class 10 Maths Quadratic Equations With Answers Ncert Books



Www Fi Muni Cz Usr Gruska Crypto13 Crypto 08 Pdf




P 2 X 2 P 2 Q 2 X Q 2 0 Solve By Completing The Square




Show The Subset Of The Vector Space Of Polynomials Is A Subspace And Find Its Basis Problems In Mathematics




Let P Q And R Have Coordinates P 2 2 2 0 Chegg Com




Quadratic Functions Functions Siyavula




P 2x 2 P 2 Q 2 X Q 2 0




Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 1 By Ayman Alam Issuu




Solution Of A Partial Differential Equation




Solve The Following Quadratic Equation P 2 X 2 P 2 Q 2 X Q 2 0 Brainly In




Ex 10 1 3 Find Distance Between P X1 Y1 Q X2 Y2 When



Solve Quadratic Equations Using The Quadratic Formula Elementary Algebra



2



Studywell Com Wp Content Uploads 21 03 Differentiationexamquestions Pdf



Solve The Following Quadratic Equation For X P 2x 2 P 2 Q 2 X Q 2 0 Sarthaks Econnect Largest Online Education Community




Using Quadratic Formula Solve The Following Quadratic Equation For X Px Square X Square P Square Q Square X Q




The Leading Order Effective Parton Density Of The Photon X Q 9 4g Download Scientific Diagram



Www Roguecc Edu Media Mathoerbooks Mth65 Pdf



If A And B Are The Roots Of X 3x P 0 And C D Are Roots Of X 12x Q 0 Where A B C D Form A Gp How




Fiitjee Question Papers From Rankers Study Material For Iit Jee By S Dharmaraj Issuu




Chapter 1 Maths 3




Solve Using Quadratic Formula P 2 X 2 P 2 Q 2 X Q 2 0 Here Means Square Brainly In



Www Jstor Org Stable




Dk Jc S Maths P2 Pamphlet




Solve These Following Quadratic Equations By Using The Quadratic Formula Sridhar Acharya S Rule 2 Brainly In




Solve Using Quadratic Formula P2x2 P2 Q 2 X Q2 0 Maths Quadratic Equations Meritnation Com




Find The Value Of P And Q If The Equation Px 5x 2 0 And 3x 10x Q 0 Have Both Roots In Common Mathematics Topperlearning Com Otbo1nn



Http Users Math Msu Edu Users Weihsuan Ss16 Hw 8 solutions Pdf




How Do You Write A Quadratic Equation In Intercept Form If You Have A Graph Printable Summary Virtual Nerd



Www Pearson Com Content Dam One Dot Com One Dot Com Uk Documents Subjects Mathematics Worksheets Chapter2 Example 6 Chapter 2 Solving Quadratics By Completing The Square Pdf




Using Quadratic Formula Solve The Following Quadratic Equation For X Px Square X Square P Square Q Square X Q



Madasmaths Com Archive Maths Booklets Basic Topics Various Polynomials Exam Questions Intro Pdf



Find The Values Of P And Q So That F X X2 3x P Ifx 1 Qx 2 Ifx 1 Is Differentiable At X 1 Studyrankersonline



3




Using Quadratic Formula Solve The Following Quadratic Equation P 2x 2 P 2 Q 2 X Q 2 0 Brainly In



1



1




P X Q Q X P 2 Maths Quadratic Equations Meritnation Com




What Is The Value Of P And Q If X 1 And X 2 Are The Factors Of X 3 3x 2 2px Q Quora



Http Www Pnp Physics Ox Ac Uk Mjohn Notes Matterlectures Pdf
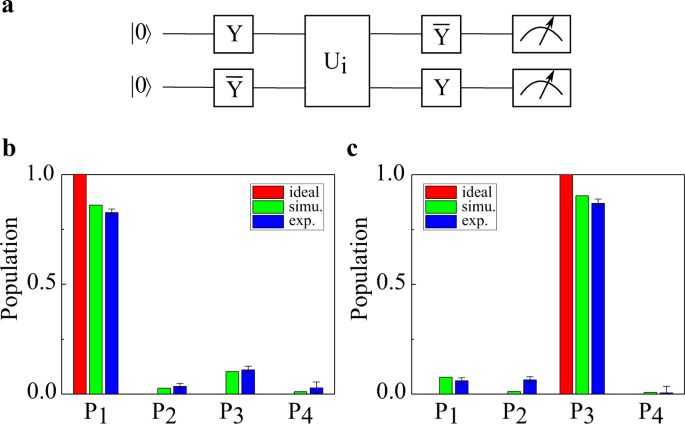



A Programmable Two Qubit Solid State Quantum Processor Under Ambient Conditions Npj Quantum Information




द व घ त स त र क प रय ग करक P 2 X 2 P 2 Q 2 X Q 2 0 क
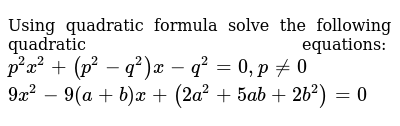



Using Quadratic Formula Solve For X P X P Q X Q 0




The Roots Of The Equation X P X Q R 2 Where P Q R Are Real Are Youtube




Solve This Equation Q P2x2 P2 Q2x Q2 0 Maths Quadratic Equations Meritnation Com




5 Charpit S Method Pdf Nonlinear System Differential Equations



Arxiv Org Pdf 1509




If The Roots Of The Equation 1 Q P 2 2 X 2 P 1 Q X Q Q 1 P 2 2



Madasmaths Com Archive Maths Booklets Further Topics Various Roots Of Polynomial Equations Pdf



2




Hydrodynamic And Kinetic Models For Spin 1 2 Electron Positron Quantum Plasmas Annihilation Interaction Helicity Conservation And Wave Dispersion In Magnetized Plasmas Physics Of Plasmas Vol 22 No 6



Solve The Following Quadratic Equation For X P2x2 P2 Q2 X Q2 0 Mathematics Topperlearning Com Cf13ivpdd




Assignments Falconer Mackay Chapters 1 And 2 1 5 1 6 2 5 And 2 6 Sanja Franic Vu University Amsterdam Ppt Download




Let A Be A Matrix And P X Anx An 18 1 Chegg Com



Exotic Ww Dibaryon States In A Molecular Picture



Cdn1 Byjus Com Wp Content Uploads 19 11 Quadratic Equation Solved Problems Pdf Converted Pdf




If P Q R X 2 Q R P X R P Q 0 Has Equal Roots Then 2 Q



Http Khudian Net Teaching Galois Gallctrs64 Pdf



Http Hsit Ac In E Learning Engineering mathematics 15mat21 Engg Maths Ii notes Pdf




Solve The Equation X 2p 2 Y 2q 2 Z 2 Mathematics 2 Question Answer Collection




Edexcel Core Mathematics C1 May 17



Math Scene Equations Iii Lesson 2 Quadratic Equations



Using Shridhar Acharya Formula Solve The Following Quadratic Equations P 2x 2 P 2 Q 2 X Q 2 0 Sarthaks Econnect Largest Online Education Community
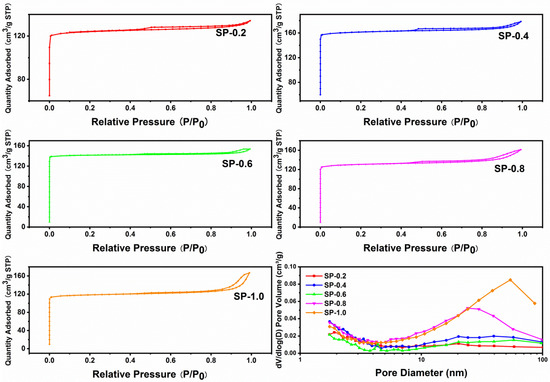



Catalysts Free Full Text Solvent Free Synthesis Of Sapo 34 Zeolite With Tunable Sio2 Al2o3 Ratios For Efficient Catalytic Cracking Of 1 Butene Html




最高のコレクション Px Q Qx P2 シモネタ



Http Hsit Ac In E Learning Engineering mathematics 15mat21 Engg Maths Ii notes Pdf



0 件のコメント:
コメントを投稿