√100以上 题目 一元 一次 方程式 223220

学习重点有关一元一次方程的概念及解一元一次方程的基本方法 学习难点灵活运用解方程的变形步骤及解应用题 一、列方程解应用题的主要步骤 1、认真审题，理解题意，弄清题目中的数量关系，找出其中的等量关系;Input 以空格分隔的一元二次方程的三个系数，双精度double类型 Output 分行输出两个根如下（注意末尾的换行）：r1=第一个根r2=第二个根结果输出时，宽度占7位，其中小数部分2位。 Sample Input 1 3 2 Sample Outputr1= 100r2= 0E 求一元二次方根 C语言#include #include int main2元一次方程式题目 be positive quotes short be creative quotes for kids be good quotes images bd r 書き込み

一元一次方程的计算和练习题 附答案 职场达人网 职场知识 职场礼仪 职场法则

题目 一元 一次 方程式

题目 一元 一次 方程式- 在初中我们就学习了关于一元二次方程的解法，也了解了关于一元二次方程的判别式、韦达定理等等。我们都知道一元二次方程是很容易解的，但一元三次方程就不同了。 所以我们故事的起因就是一位意大利数学家 费罗 。他在长期的钻研中找到了无二次项一元一元二次方程练习题 作业帮： 1、(1)是(2)是(3)不是(4)不是 2、(1)一般式2x 3x5=0,二次项系数2,一次项系数3,常数项5(2)一般式x 2x1=0,二次项系数1,一次项系数2,常数项1(3)一般式2x 9x14=0,二次项系数2,一次项系数9,常数项14(4)一般式(1√2 )x (1√2 )x=0,二次项系数1√2 ,一次项

一元一次方程50道练习题 带答案 50道方程题下载 Word模板 爱问共享资料

 一元二次方程根的判别式推导和基本题目ppt,一 元 二 次 方 程 的根的判别式 目的要求 知道什么是一元二次方程的根的判别式。 会用判别式判定根的情况。 例 不解方程，判别下列方程的根的情况： 课堂练习 * * 新课教学 现在我们来研究方程 变形得到的 首先应说明，对上述方程的左边，是个平 一元二次方程 教学内容 一元二次方程概念及一元二次方程一般式及有关概念． 教学目标 2 了解一元二次方程的概念；一般式axbxc=0（a≠0）及其派生的概念；?应用一元二次方程概念解决一些简单题目．已知反比例函数的图象如图，则一元二次方程根的情况是 A有两个 开始做题 下列说法中，正确的是 A．9的算术平方根是3B．有一个内角为40°的两 开始做题 已知实数a≠b，且a、b是方程x25x1=0的两根，则的值为 A．23B．﹣2 开始做题 已知：关于x的方程x22x=3

 2、 2 、一元二次方程的一般式： 3、 由以上问题得到 3 个方程, 由学生观察归纳这 3 个方程的特征, 给出名称并类比一元一次方程的定义, 得出一元二次方程的定义 活动中教师应重点关注 (1) 引导学生观察所列出的 3 个方程的特点;解一元二次式的各种方法 ： 解一元二次方程一般有以下四种方法 直接开平方法,因式分解法,配方法,求根公式法 (1)当方程形如(xa)2=b(b≥0)时,可用直接开平方法;一元三次方程怎么解(高中方法),最好举几个例子,比如x∧3 3x∧24=0： (1) 66x17y=3967 25xy=10 答案x=48 y=47 (2) 18x23y=2303 74xy=1998 答案x=27 y=79 (3) 44x90y=7796 44xy=3476 答案x=79 y=48 (4) 76x66y=40 30xy=2940 答案x=98 y=51 (5) 67x54y=8546 71xy=5680 答案x=80 y=59 (

一元二次方程；解一元二次方程练习题，针对初三第1周，一元二次方程；解一元二次方程精选道练习题，精选，精练，详解_数学周周练。 题量：59题 时间：316分钟 总分：595分 查看题目列表 考查知识点：一元二次 第32周 中考复习—代数式 1/4 直接开平方法：顾名思义，就是直接开平方求解一元二次方程的方法，运用的原理是平方的逆运算，是解一元二次方程的主要方法之一，适用于没有一次项的一元二次方程。 2/4 因式分解法：根据名字我们不难猜出它的用法，就是把一个多项式化为几个整式 一元三次方程题目及答案 从小学到大学，数学都是最难的科目之一，家长从小学开始也会格外注意孩子，在数学科目上的表现和教学进度。 近段时间，某小学数学家长群里的聊天信息走红网络，不少网友都在调侃群里的家长。 数学术语"一元一次方程"走红

初一 一元一次方程 应用题归类分析 你可以试试

第3章一元一次方程检测试题 一元一次方程题及过程 次方问题

 初二数学一元二次方程专题复习题 一元二次方程是中学代数的重要内容之一，是进一步学习其他方程、不等式、函数等的基础，其内容非常丰富，本讲主要介绍一元二次方程的基本解法． 方程ax2bxc=0(a≠0)称为一元二次方程． 一元二次方程的基本解法有开平方法、配方法 初三一元二次方程30个题目及详解 —— 例1解方程(1)(3x1)2=7 (2)9x224x16=11 分析(1)此方程显然用直接开平方法好做,(2)方程左边是完全平方式(3x4)2,右边=11>0,所以 此方程也可用直接开平方法解 (1)解(3x1)2=7* ∴(3x1)2=5 ∴3x1=±(注意不要丢 一元一次方程测试题及答案doc,第 PAGE 1 页 共 NUMPAGES 4 页 第六章 一元一次方程测试题 A卷 一、填空题 1、若与互为相反数，则

一元一次 新人首单立减十元 21年7月 淘宝海外

人教版初中数学七年级上册第三章 一元一次方程 单元测试题 含答案解析 七七文库www 77wenku Com

______ 一次方程一般表达为axb=c,其中a,b,c为常数方法主要是移项ax=cb1当a≠0时x= (c一b)/a2当a=0,且cb=0时x为任意解3当a=0,且cb≠0时方程无解 ______ 化二元一次方程为一元一次方程解,常用方法加减消元法和代入消元法 关于 \(x\) 的方程 \(\displaystyle (m1)x^{m^21}(m3)x1=0\) 是一元一次方程，则 \(m=\) \(0或1\) 对于不定次项，要考虑不存在（系数为0）和1次或0次的情况 2 一元一次方程式题目 更新日期： 作者： 更新日期： 初一100道一元一次方程计算题带答案 —— 3X5X=48 X=614X8X=12 X=2 6*52X=44 X=7X50=50 X=5 286X= X=X=10 X=1 4y2=6 Y=1 x32=76 X=443x6=18 X=4168x=40 X=32x8=8 X=84x3*9=29 X=98x3x=105 X=21 x6*5=42 X=72 x5=7 X=22x3=10 X=7/212x9

17年小升初衔接数学一元一次方程应用题 小升初衔接 奥数网

17 3可化为一元一次方程的分式方程练习题 试题 16 3可化为一元一次方程的分式方程 初中华师大版13版 数学中国网 Mathschina Com

 一元二次方程100道计算题练习 =166、2（2x－1）－x（1－2x）=0 =648、5x –72=010、3x(x2)=5(x2) 11、（1－3y） 2（3y－1）=012、x 6x－5=014、x 3x1=017、3x 2x4=024、x 3=4x25、3x ＋8x－3＝0（配方法） 26、(3x＋2)(x＋3)＝x＋14 27、(x1)(x8)=12 28、2(x－3) －929、－3x ＋22x－24＝030、（2x1） 3（2x1）2=031、2x －9x＋8＝032、3（x5） =x(5x)33、(x＋2) ＝8x34、(x－2) 3135 2365 补充练习：一一元一次方程式也被稱為线性 方程，因為在笛卡尔坐标系上任何一個一次方程的圖形都是一條直线。 组成一次方程的每一项必須是常数或者是一个常數和一个变量的乘積。 且方程中必須包含一个變量，因為如果没有變量只有常數，式子則是代数式而非方程式。 如果一次方程式中只包含一个文字符 简介：19一元二次方程判别式中考解答题专练（解析版） 一、解答题 1．（18·湖北中考真题）已知关于x的一元二次方程x2﹣（2k﹣1）xk2k﹣1=0有实数根． （1）求k的取值范围； （2）若此方程的两实数根x1，x2满足x12x22=11，求k的值．

青岛版数学七年级上册第7章 一元一次方程 检测题 名师指导 初中 山东启达教育网

初一应用题 一元一次方程应用题类型总结 习题二及答案15日更新 初中年级 家长帮

 ∴x5=0或x2=0 (转化成两个一元一次方程) ∴x1=5,x2=2是原方程的解 2x23x=0 x(2x3)=0 (用提公因式法将方程左边分解因式) ∴x=0或2x3=0 (转化成两个一元一次方程) ∴x1=0,x2=是原方程的解 注意：有些同学做这种题目时容易丢掉x=0这个解,应记住一元二次方程有两个解 一元一次方程练习题(150道,包括答案) —— 第3章 一元一次方程全章综合测试 (时间90分钟,满分100分) 一、填空题(每小题3分,共24分)1已知4x2n55=0是关于x的一元一次方程,则n=_____2若x=1是方程2x3a=7的解,则a=_____3当x=_____时,代数式 x1和 的值互 一元一次方程，同学们将会在初一接触到它，实际，解一元一次方程还是很简单的，下面小编就为你解一道一元一次方程，相信聪明的你看完小编的例题后就能够举一反三啦！ 工具/原料 more 本子 笔 方法/步骤 1 /6 分步阅读 第一，列出方程。当我们解一道方程

解一元一次方程50道练习题带答案 豆知网

一元一次方程的计算和练习题 附答案 职场达人网 职场知识 职场礼仪 职场法则

初中数学一元二次方程知识点整理 一、定义和特点 1、一元二次方程：含有一个未知数，并且未知数的最高次数是2的整式方程叫做一元二次方程。 2、一元二次方程的一般形式：ax的平方bxc=0 (a 0)，它的特征是：等式左边加一个关于未知数x的二次多 211 一元二次方程 初中数学 人教11课标版 1教学目标 了解一元二次方程的概念；一般式ax2bxc=0（a≠0）及其派生的概念； 应用一元二次方程概念解决一些简单题目． 1．通过设置问题，建立数学模型， 模仿一元一次方程概念给一元二次方程下定义．说明书 配方法解一元二次方程练习题 222 降次——解一元二次方程（2） 双基演练 1．用适当的数填空： （1）x23x________=（x_______）2 （2）a（x2x_______）=a（x_______）2 2．将一元二次方程 x22x4=0 用配方法化成（xa）2=b 的形式为_______，?所以方程的根为_________． 3．如果关于 x 的方程 x2kx3=0 有一个根是1，那么 k=________，另一根为______． 4．将二次三项式 2x23x5

一元一次方程道题 美丽考试间

数学7上 非负数在解一元一次方程中的应用考试题 教育资讯 娱乐新闻网

 二元一次方程组练习题40道带过程 ？ >> 1) 66x17y=3967 25xy=10 答案x=48 y=47 (2) 18x23y=2303 74xy=1998 答案x=27 y=79 (3) 44x90y=7796 44xy=3476 答案x=79 y=48 (4) 76x66y=40 30xy=2940 答案x=98 y=51 (5) 67x54y=8546 71xy=5680 答 解一元二次方程步骤： ①求b4ac的值，大于0有解，小于0无解 ②有公因式先提公因式 ③公式法（完全平方公式，平方差公式） 解一元一次方程的一般步骤：（1） 去分母：方程两边同时乘以各项分母的最小公倍数；例题6：为下面方程去分母：；（2） 去括号：可先去小括号，再去中括号，最后去大括号（也可以按照自己擅长的方式去括号）；例题7：去括号：2 (x3)－5 (1－x)=3 (x－1)（3

解一元一次方程计算题每天训练 15分钟 每日头条

一元一次方程 搜索结果 哔哩哔哩 Bilibili

 初中数学教学案例一元一次方程一：教材分析： 1：教材所处的地位和作用： 本课是在接一元一次方程的基础上，讲述一元一次方程的应用，让学生通过审题，根据应用 题的实际意义，找出相等关系，列出有关一元一次方程，是本节的重点和难点，同时也是本 章节的重难点。 1一元一次方程： 只含有一个未知数，并且未知数的次数是1，并且含未知数项的系数不是零的整式方程是一元一次方程。 2一元一次方程的标准形式： axb=0 (x是未知数，a、b是已知数，且a≠0)。 3条件：一元一次方程必须同时满足4个条件： (1)它是等式; 一元二次方程题目集合最少100题,： (1)x^29x8=0 答案x1=8 x2=1 (2)x^26x27=0 答案x1=3 x2=9 (3)x^22x80=0 答案x1=8 x2=10 (4)x^210x0=0 答案x1= x2=10 (5)x^2x96=0 答案x1=12

初一数学一元一次方程的测试及答案 Doc 文档分享网

四年级奥数题 简单一元一次方程例题及巩固练习 四年级奥数题 奥数网

 774 本 题目 要 求一元二次方程 a*x2＋b*x＋c＝0 的 根 ，结果保留2位小数。输入格式：输入在一行中给出3个浮点系数a, b, c，中间用空格 分 开。 输出格式： 根 据系数情况，输出不同结果：1)如果方程有两个不相等的实数 根 ，则每行输出一个 根 ，先大后小； 2)如果方程有两个不相等复数 根 ，则每行按照格式"实部虚部i"输出一个 根 ，先输出虚部为正的，后输出虚部为

选择题和一元一次方程 Nbsp 综合作业 移商院

人教版七年级数学解一元一次方程练习题 松鼠文库

一元一次方程式的解题方法与技巧 自学习网

一元一次解方程50道题 西瓜视频搜索

初中数学 一元一次方程常考的13种应用题 掌握考高分 知乎

七年级数学一元一次方程50道练习题 含答案 侵权

初一上册数学第三章 一元一次方程 练习题 初一数学 中考网

关于一元一次方程的复习课教学反思1500字 范文118

七年级数学a卷题 第6章一元一次方程 衡课网 衡课网

七年级数学一元一次方程打折销售经典练习题及答案

一元一次方程实际问题解题方法 百度经验

一元一次不等式练习题 附答案 职场达人网 职场知识 职场礼仪 职场法则

一元一次方程练习题 预初年级 上海奥数网

解一元一次方程计算题训练下载 Word模板 爱问共享资料

一元一次方程练习题及答案 松鼠文库

國中數學認識一元一次方程式 Youtube

解一元一次方程50道练习题 3326学习网

50道一元一次方程带解题步骤 百度经验

七年级数学一元一次方程应用题专题练习 初一数学 中考网

解一元一次方程50道练习题 带答案 Doc 在线文库www Lddoc Cn 在线文库www Lddoc Cn

一元一次方程应用题公式汇总 知乎

一元一次方程计算精选无答案 奇酷网 Qikuw Com

一元一次方程计算题难 解一元一次方程道经典练习题 包含各种复杂方程 简明教程

完了しました 一元一次方程式問題 一元一次方程式問題

一元一次方程题库 万图壁纸网

一元一次方程应用题分类 101教育初一手机端

请提供一些一元一次方程去分母练习题 快资讯

北师大版七年级数学上册第五章 一元一次方程 练习题及答案 莲山课件

初一数学一元一次方程和差倍分练习题及解析 上海爱智康

关于x的一元一次方程ax B的解法 网上竟然有那么多的争论 知乎

一元一次方程6 1 6 2水平测试 1 华七下第六章 6 2解一元一次方程 初中华师大版 数学中国网

七上数学第三章 一元一次方程 知识点 名师精选练习题 可打印 楠木轩

中考数学试题考点8 一元一次方程 常见题型一定要掌握 中考 学习资料大全 免费学习资源下载

解一元一次方程50道练习题经典 强化 带答案 豆知网

初中一元一次方程5大解题技巧 8大例题 赶紧掌握 教育频道 手机搜狐

人教版初一数学上册 解一元一次方程 二 去括号与去分母同步试题与答案 黄冈作业本 黄冈中学试卷 黄冈题库

解一元一次方程计算题每天训练 15分钟 自学习网

版一元一次方程的解法练习题 Docx 教育文库 教育资源网 新时代文库www Xsdwk Com 教育文库 教育资源网 新时代文库www Xsdwk Com

解一元一次方程50道练习题带答案资料 豆知网

必备初一上册数学课后练习题 一元一次方程 数学同步练习 精品学习网

精心整理 一元一次方程基础练习题下载 Word模板 爱问共享资料

列一元一次方程解应用题专项练习180题有答案 豆知网

七年级数学a卷题 第6章一元一次方程 衡课网 衡课网

一元一次方程不等式应用题一元一次方程 不等式

小学五年级方程练习题下载以及教学 宝宝学习网

一元一次方程计算题80道直接打印 豆知网

怎样列一元一次方程 西瓜视频搜索

方程题100道 万图壁纸网

十道一元一次方程的题求10道以上一元一次方程的应用题

解一元一次方程习题精选附答案 松鼠文库

人教版 初一数学一元一次方程练习题 数学练习题 成都中考网

1

一元一次方程 搜狗图片搜索

一元一次方程高频考点 经典题型演练 楠木轩

初一数学一元一次方程填空求解急急 图片欣赏中心 急不急图文 Jpjww Com

小学一元一次方程练习题 整数 Pdf 万象文库www 2wx Com

名師課輔網 一元一次方程式技巧

数学7上 一元一次方程怎么解 这题看着很复杂 懂得技巧好简单 网易视频

七年级数学一元一次方程50道练习题 含答案 侵权

19年初一寒假数学提升练习题 解一元一次方程 北京爱智康

真题分类 一元一次方程 在中考时会怎么考 3u文域

1

初一数学一元一次方程概念与解题方法例题解析 三好网

一元一次方程应用题题型 初中电子课本网

一元一次方程练习题 道 分享答案一元一次方程练习题分享30道 励志名言网

专题突破 六种一元一次方程解法与技巧 人人焦点

中考数学指导 一元一次方程练习题及答案 一元一次方程资讯 新东方在线移动版

1

解一元一次方程50道练习题 经典 强化 带答案 松鼠文库

初一数学一元一次方程测验 Doc 文档分享网

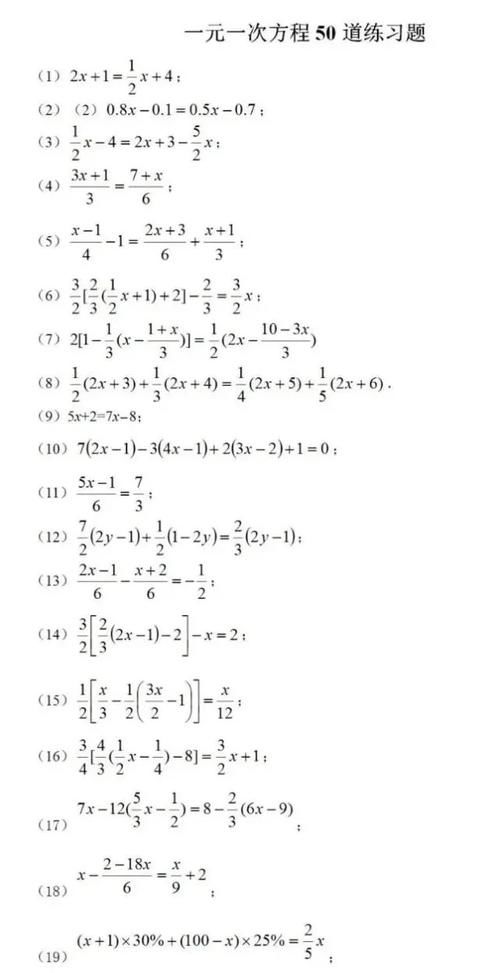
一元一次方程100道带答案

方程七上数学 解一元一次方程道经典练习题 包含各种复杂方程 利财股票网

完整的题型 完美的解法 全解一元一次方程 初中数学 学习资料大全 免费学习资源下载

初中奥数一元一次方程练习题 方程和不等式 精品学习网

一元一次方程计算题书目 一元一次方程计算题作品 京东图书

初一数学一元一次方程 搜狗图片搜索

100道一元一次方程计算题 绿色文库网

一元一次方程例题解析求40道一元一次方程计算题

一元一次方程式應用題 1 1 2 Youtube

7题求解 一元一次方程 8题求解 一元一次方程 数学作业 解题作业帮

一元一次方程计算题

分数方程计算题100道 万图壁纸网

解一元一次方程100题 七年级数学 吾爱数学首页 初中数学学科资源 初中数学备课资源下载

一元一次方程50道练习题 带答案 50道方程题下载 Word模板 爱问共享资料

初一高中解一元一次方程 合并同类项与移项 练习题30道13南充技能素质数学年 高中课题目

Search Q E4 B8 80 E5 85 E4 B8 80 E6 Ac A1 E6 96 B9 E7 A8 8b E7 E4 B9 A0 E9 98 E5 B0 8f E5 Ad A6 Tbm Isch

一元一次方程计算题 绿色文库网

初一上数学期末复习 一元一次方程及应用题视频讲解学案 哔哩哔哩